该技术遵循“明显配对”原则。但在这种情况下,为了解决数独问题,我们需要找到 3 个单元格,其中的数字必须相同。
该方法看似复杂,但实际上很容易操作。让我们看下面的例子。该行中没有足够的数字:1、2、6、7、9。使用最后可能的数字方法,我们知道在中间的 3x3 块中,数字 1 将保留,而在最右边只能有数字 7。这意味着我们可以从左侧块的左下线划掉这些数字。
我们已经从候选者中排除了 1 号和 7 号。左侧块的行将包含候选数字:2、6 和 9。这些将是我们的“明显的三”。
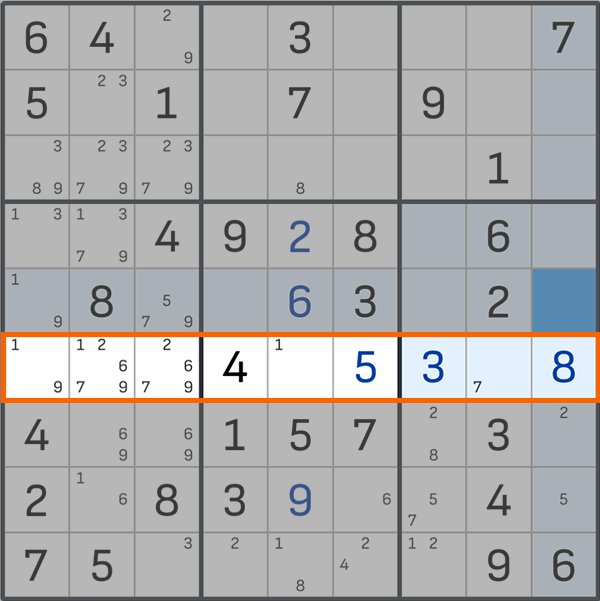
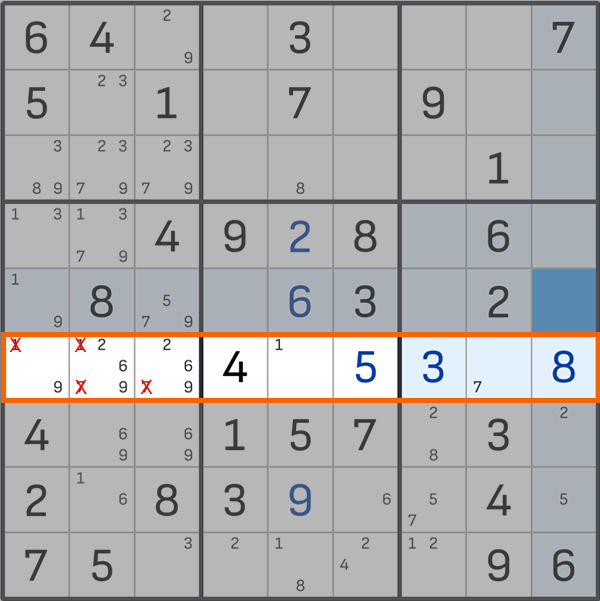
现在让我们看看左边的 3x3 块。底部三个单元格中只能放置 2、6 或 9,不能放置其他数字(根据数独规则)。因此,我们可以从剩余的单元格中划掉这些数字 - 我们删除 9(此块中不再有 2 和 6)。在中间左侧的单元格中,我们有一个“明显的单一” - 1。我们输入它。
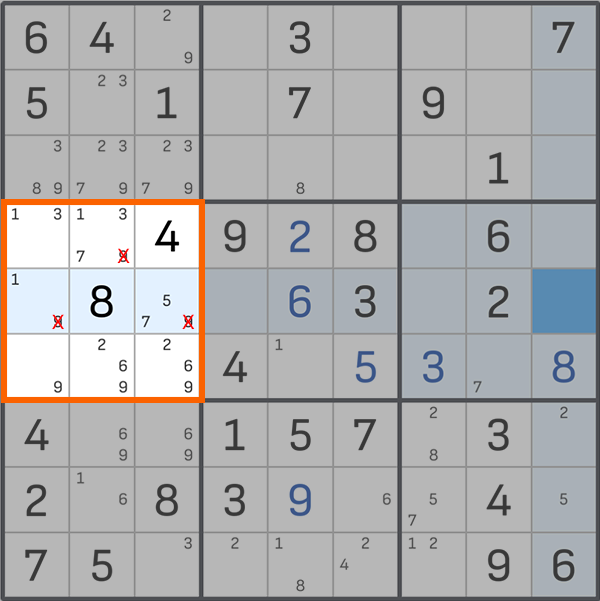
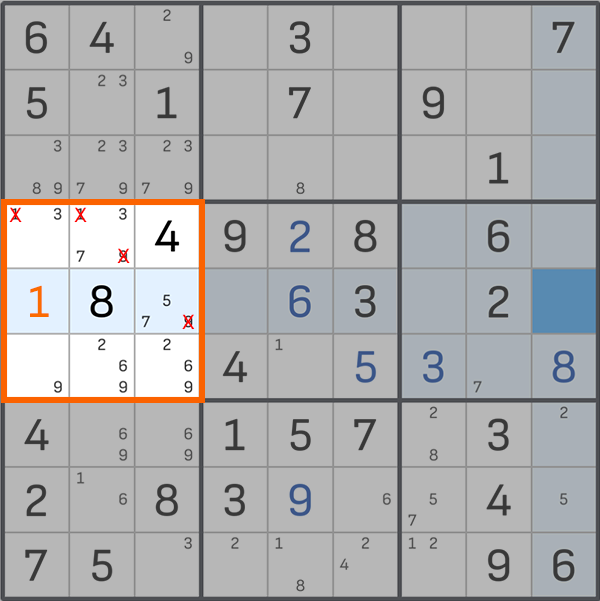
接下来,从所有音符中删除 1,并输入数字 3 和 9。
显式三元组方法允许您缩小搜索范围并最大限度地减少由于值重复而导致错误的风险。
如果您已成功掌握此方法并学会了如何解决简单数独,请继续学习更复杂的谜题,并学习其他策略。