让我们看一下解决数独的基本策略,这些策略将对初学者和专业人士都有帮助。在下面的说明中,我们将分享如何快速轻松地解决难题的工作技巧。
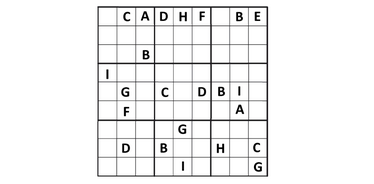
搜索“唾手可得的果实”
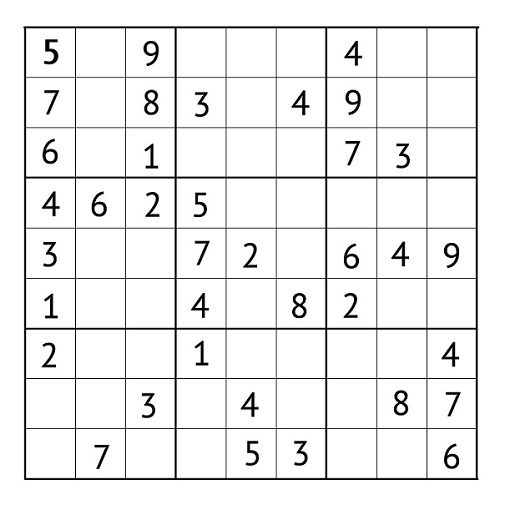
该策略基于消除过程,以选择需要的数字并将其放置在网格上的方格中。玩家查看场上已经有哪些值,然后决定添加新的值。
查看中间行(左列)的方块。这里我们已经放置了数字 4、6、2、3、8、5、1 和 7。自然,通过消除法,我们知道缺少一个 9。输入数字 9 后,您就可以继续解决问题了。
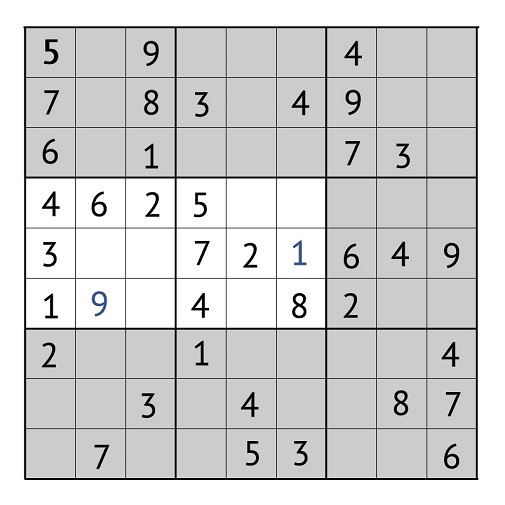
但是让我们看看我们还有哪些“唾手可得的果实”。我们建议注意贯穿中央行的线。它也缺少一位数字!有 3、8、5、7、2、6、4 和 9。通过消除法,我们知道我们需要一个。我们将其放在一个空单元格中。
“水果”的搜索策略已经取得成果。现在我们有一个已填充 +2 个单元格的数独网格。
研究邻近的方块
将 9 和 1 相加后,我们发现不再有此类低果实的免费物品。好的,我们尝试继续。中心广场的中间柱子引人注目。数独的作者已经填满了:1、2、4、5、7 和 8。通过消除法,我们知道我们缺少数字 3、6 和 9。但如何正确放置它们呢?
为了回答这个问题,让我们继续。我们看到左侧和下方的相邻方块。我们从需要输入数值 3、6 和 9 开始。左边的方块中已经有一个六,而我们在底部看到一个三。因此,在中间方块的右上角,你需要写上数字九。这种方法称为排除法。它不仅用于日常生活,还用于国际锦标赛。
我们继续前进,尝试找到“放置” 3 和 6 的位置。左侧的方块顶行已经有一个 6,因此我们排除了将 6 放置在中央方块顶行的可能性。消除过程表明这里只能插入三个。
完整的数独网格如下所示:
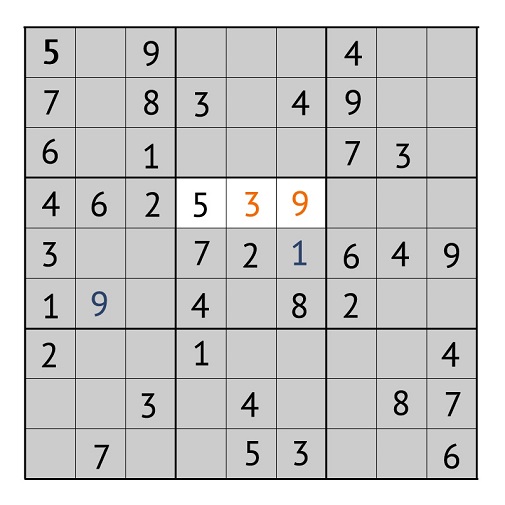
当然,例如,我们采用了简单的谜题,其中作者已经填写了几乎所有的字段。但是“低垂的果实”策略可应用于数独的任何级别。只需寻找明显的解决方案和带有填充单元格的方块/列/线。