數獨這個數字謎題最早由瑞士數學家萊昂哈德·歐拉於18世紀提出,但直到20世紀80至90年代才真正普及起來。所謂的「拉丁方陣」或「魔方陣」能夠提升專注力、邏輯思維與分析能力,也是一種有益的休閒活動。
傳統數獨是一個9×9的方格,被劃分為每邊3格的小正方形區域。整個遊戲的基礎是一個81格的網格。遊戲有不同的難度級別,取決於初始給出的數字數量和解題方法。遊戲規則很簡單:將數字填入空格,確保每一行、每一列及每一個小方格內,數字都不重複。
除了9×9的經典數獨外,還有其他變化形式,從4×4到25×25的格子不等。此外還有一些附加條件、特定區塊、以及非方形的幾何形狀等。我們來看看其中幾個受歡迎的變體。
數獨的種類
- 數獨 X
這種玩法是NxN(通常為9×9)格的正方形。它由N(9)個小區塊組成,每個區塊又包含N(9)個小格子。遊戲開始前,部分格子已填入數字。
玩家的任務是在其餘空白格中填入1到N(9)之間的數字。規則是:每列、每行與每個區塊(9×9)中,每個數字只能出現一次,不能重複。
此外,數獨 X 的兩條主對角線上也不得出現重複的數字。
- 殺手數獨
殺手數獨本質上是「數獨」與「加加樂」(Kakuro)兩種遊戲的結合。表面上它看起來像一般的數獨,但與經典版不同的是,它包含了額外的區域,這些區域內數字總和必須等於給定值,就像加加樂一樣。解題時常用一個重要事實:1到9的總和永遠是45。這有助於在有多個相鄰區塊且僅剩一格空位時,計算正確的數字。只需從45(或90、135等)中扣除已知區塊的總和即可。
- 奇偶數獨
在此變體中,遊戲提供每個格子的奇偶性提示。含有奇數的格子通常會用圓形標示。
玩家的任務是根據傳統規則填入1到9的數字,確保每行、每列及每個區塊內數字不重複。
- 點標數獨
此類型的數獨在格子之間的邊界上標有黑白點。白點表示兩個相鄰數字相差為1,黑點表示一個數字是另一個的兩倍。對於1和2這樣符合兩種條件的組合,可以用黑點或白點表示。
- 拼圖數獨
拼圖數獨是NxN(通常為9×9)格的正方形。它由N(9)個小區塊組成,每個小區塊包含N(9)個小格子。部分格子已填入數字。
玩家需要將1到N(此處為9)的數字填入空格,並確保每行、每列與每個區塊內的數字不重複。
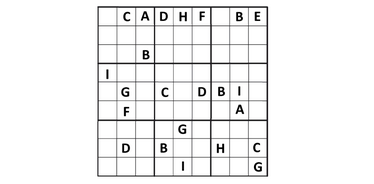
- 字母數獨
這是一種改良版數獨,用字母代替數字進行填格。此變體被稱為「Wordoku」。它使用9個字母,類似於傳統數獨中的9個數字。遊戲目標與規則相同:每行、每列與每個3×3區塊中,每個字母只能出現一次,不得重複。
- 武士數獨
武士數獨是由5個重疊的9×9數獨網格組成。每個網格皆遵循經典數獨規則。玩家需在所有空白格中填入1到9的數字,並確保每行、每列、每個3×3區域內無重複。
此類型的獨特之處在於,這五個網格無法分開解答,它們共享唯一的整體解。
- 窗格數獨(Windoku)
這種變體在標準9×9網格中加入了4個彩色標示的附加區塊,稱為「窗格」。
這些窗格與標準的行、列和3×3區塊重疊,使遊戲更具挑戰性。除了遵循經典規則外,這4個窗格也必須包含1到9的所有數字,且不得重複。
- 大小數獨
這是經典數獨的另一種改編。此類型中,初始網格不含任何預設數字,而是用「>」和「<」等比較符號來表示相鄰格子中數字的大小關係。
- 星號數獨
此類型的網格中,有一個顏色標示的特殊區域,形狀類似星號(*),共9格。這些格子也需按照傳統數獨規則填入1到9的數字。