数独这种数字谜题最初由瑞士数学家莱昂哈德·欧拉在18世纪发明,但直到20世纪80至90年代才开始流行。所谓的“拉丁方阵”或“魔方阵”有助于提升专注力、逻辑思维和分析能力,同时也是一种有益的休闲活动。
传统的数独是一个9×9的正方形,被划分为每边为3格的小正方形区域。整个游戏建立在由81个格子组成的网格上。游戏有不同的难度级别,取决于初始数字的数量和解题方式。游戏规则很简单:在空格中填写数字,确保每一行、每一列和每一个小方格内的数字都不重复。
除了9×9的经典数独,还有其他变种,从4×4到25×25不等。也有带有附加条件、特殊区域或非正方形几何形状的版本。下面我们来看看一些流行的变种。
数独的种类
- 数独 X
这种玩法是一个NxN(通常为9×9)格的正方形。它由N(9)个小区块组成,每个区块又包含N(9)个小格子。在游戏开始前,一些格子里已经填写了数字。
玩家的任务是在剩下的空格中填写1到N(9)的数字。规则是:在每一列、每一行和每一个区块(9×9)中,每个数字只能出现一次,不得重复。
此外,数独 X 的两条主对角线上的数字也不得重复。
- 杀手数独
本质上是“数独”和“加加乐”(Kakuro)两种游戏的结合。杀手数独外观上与普通数独相似,但与经典版本不同,它包含了额外的区域,这些区域中所有数字的总和必须等于指定的数值,就像在加加乐中一样。解题时经常使用的一个事实是:1到9的总和始终为45。这有助于在一些相邻区域只有一个空格时,精确计算出该格的数字。只需用45(或90、135等)减去已知区域的总和即可。
- 奇偶数独
在这种数独中,会提供格子内数字是奇数还是偶数的信息。含有奇数的格子会用圆圈标注。
你的任务是按照传统规则填写1到9的数字,确保每一行、每一列和每一个区块中每个数字只出现一次。
- 带点数独
在这种类型中,格子之间的边界会有黑点或白点。白点表示相邻格子的数字相差1,黑点表示其中一个数字是另一个的2倍。对于1和2这种同时符合两个条件的组合,点可以是黑色或白色。
- 拼图数独
拼图数独是一个NxN(通常为9×9)的正方形,由N(9)个小区块组成,每个区块包含N(9)个格子。一部分格子在游戏开始前已填入数字。
该类型的任务是在空格中填写1到N(在此为9)的数字,确保每一行、每一列和每一个区块中数字不重复。
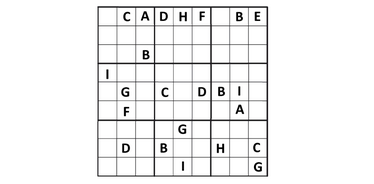
- 字母数独
这是一个用字母代替数字的数独变体。这种玩法被称为“Wordoku”。游戏中使用9个字母,就像传统数独中使用9个数字一样。游戏规则与数独完全一致:每一行、每一列和每一个3×3区块必须包含全部的字母且不重复。
- 武士数独
武士数独由五个互相重叠的9×9数独网格组成。每个网格都遵循经典的数独规则。玩家的任务是在所有空格中填写1到9的数字。每一行、每一列和每一个3×3区块中的数字不能重复。
其独特之处在于:这五个数独网格不能单独解出,它们共享一个唯一的整体解。
- 窗口数独(Windoku)
这种数独在标准9×9网格的基础上增加了四个颜色标注的额外区域,称为“窗口”。
这些窗口与标准的行、列和3×3区块重叠,使谜题更具挑战性。除了标准规则外,这四个窗口也必须包含1到9的所有数字且不重复。
- 大小数独
这是经典数独的另一种变体。这种谜题中,初始网格没有预设数字,而是用“>”和“<”等比较符号来表示相邻格子的数字大小关系。
- 星号数独
这个数独网格中有一个颜色标注的特殊区域,由9个格子组成,其形状像星号(*)。在这些格子中,也需要按照经典数独的规则填写1到9的数字。