The "Y-Wing" method is a pretty advanced way of solving Sudoku puzzles. It's a good fit for experts who are up for challenging themselves with hard Sudoku puzzles.
The "Y-Wing" method is pretty similar to the "X-Wing" method. The main difference is that it uses three corners instead of four.
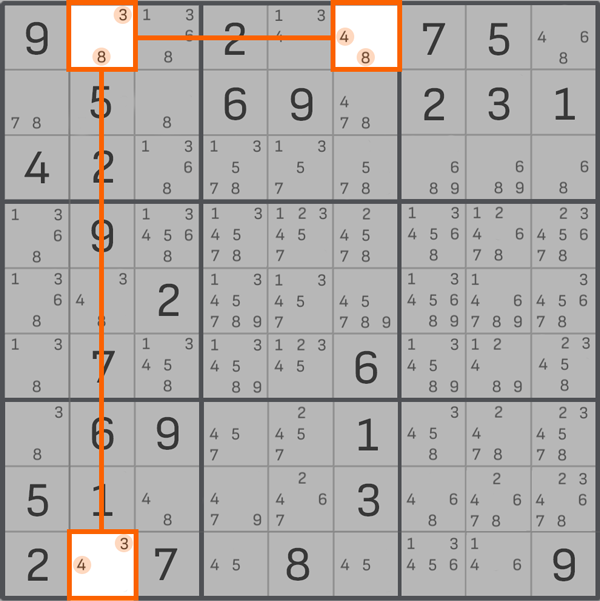
Let's take a look at an example. Let's find a cell with just two notes, 3 and 8. We'll call this cell the "pivot."
Next, we need to find two more cells in which we have left two notes each. These are called "branches." The thing to keep in mind is that the "branches" have to be in the same column, row, or block as the "pivot." Also, one of the two numbers in each "branch" has to match the number in the "pivot," and the second number has to be the same for both "branches." In our example, these are the cells with the notes 4-8, 3-4 (where 3 and 8 match the notes in the stem, and 4 is in both branches).
Next, we need to identify where the branches intersect. This means we need to add more lines (like in the example below).
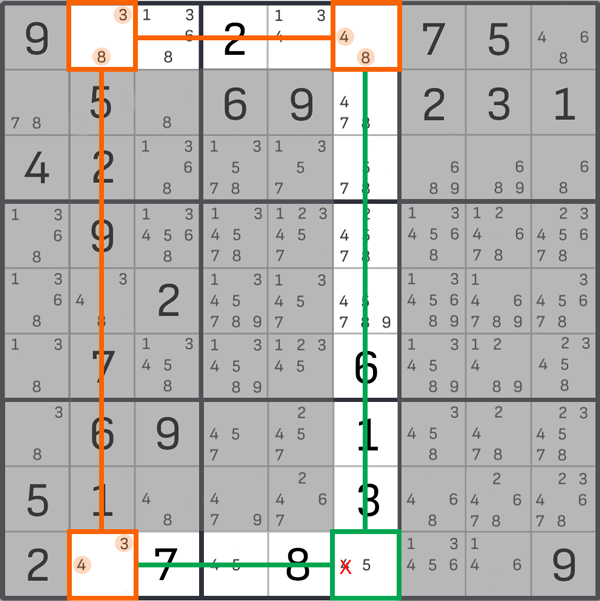
Once we've mentally drawn the lines and outlined the Sudoku field, we can see that the intersection cell is at the bottom. It has two numbers, 4 and 5. We know that a double is formed both vertically and horizontally. In this case, we can remove the 4 from the intersection cell, leaving a 5. So the "Y-Wing" method has helped us fill at least one cell (and we know exactly what a 5 should be in it). This makes it easier to fill other blocks, columns, and rows in the Sudoku.